Άπειρο μέσα στο άπειρο; Μας κάνουν πλάκα οι φυσικοί;
Αντώνης Κοτσαμπασέρης
Από το παρόν στο μέλλον, από την αιτία στη συνέπεια, η ζωή μας βρίσκεται συνεχώς σε μία αέναη κίνηση προς μία άγνωστη κατεύθυνση. Ο άνθρωπος, με την πολύπλοκη συνείδηση που του έδωσε η φύση, έχει το προνόμιο αλλά και την “κατάρα” να αντιλαμβάνεται το χθες, το αύριο και, κατ’ επέκτασιν, το τέλος. Υπήρξε από την αρχαιότητα διακαής πόθος του είδους μας να μάθει πως ξεκίνησε αλλά και πως θα τελειώσει ο κόσμος που μας φιλοξενεί..
Αψηφώντας το φόβο και τις δυσκολίες, κάποιοι γενναίοι και εγγενώς περίεργοι άνθρωποι αποφάσισαν να εξερευνήσουν το άγνωστο και να μη μείνουν στις εύκολες και τυποποιημένες απαντήσεις που προσφέρουν ορισμένοι σκοταδιστικοί οργανισμοί. Αυτή η απόφαση μας έδωσε τη φυσική, τα μαθηματικά, συνολικά τις φυσικές επιστήμες, ακόμη και τη φιλοσοφία, αλλά και μια παγκόσμια επιστημονική κοινότητα που συνεχίζει την εξερεύνηση. Όπως συχνά συμβαίνει, σήμερα βρισκόμαστε με περισσότερες ερωτήσεις απ’ όσες είχαμε όταν ξεκινήσαμε, αν και η πρόοδος που έχει επιτευχθεί στη σύντομη ιστορία της επιστήμης είναι εντυπωσιακή.
Το αρχικό πρόβλημα έχει πάρει πολύ μεγαλύτερες διαστάσεις, κυριολεκτικά και μεταφορικά. Τα σύνορα του κόσμου μας επεκτάθηκαν ραγδαία όταν μάθαμε πως ο πλανήτης μας είναι ένας συνηθισμένος βράχος που περιστρέφεται γύρω από ένα συνηθισμένο αστέρι, ανάμεσα σε δισεκατομμύρια άλλα, τα οποία αποτελούν τον γαλαξία μας.
Έπειτα, ανακαλύψαμε πως υπάρχουν αμέτρητοι γαλαξίες που κινούνται εδώ και δισεκατομμύρια χρόνια μέσα σε έναν -ίσως- άπειρο διαμετρικά χώρο, τον οποίο ονομάσαμε σύμπαν. Μάλιστα, το σύμπαν μας, όχι μόνο είναι αφάνταστα μεγάλο, αλλά διαστέλλεται με επιταχυνόμενο ρυθμό και, όπως όλα δείχνουν, κάθε γαλαξίας θα καταλήξει τόσο μακριά από τον κοντινότερο γείτονα του, που ουσιαστικά θα καταδικαστεί σε αιώνιο σκοτάδι. Όπως είπε και ο Albert Camus, “Απελπισία!”.
Πολυσύμπαν
Σαν να μην έφταναν όλα αυτά, οι φυσικοί έρχονται να προτείνουν μία ακόμη πολυπλοκότητα. Το σύμπαν που περιέγραψα παραπάνω, λένε, είναι μόνο ένα από τα άπειρα και παράλληλα πιθανά σύμπαντα, τα οποία συνυπάρχουν συνολικά σε ένα αφηρημένο μαθηματικό και, υποθετικά, φυσικό μοντέλο το οποίο αποκαλούμε πολυσύμπαν, ή όπως είναι ευρέως γνωστό, multiverse. Μία από τις πιο δύσκολες έννοιες της σύγχρονης φυσικής, που προκαλεί τη λογική, και σε κάποιες περιπτώσεις, την ηθική που έχουμε αναπτύξει σαν είδος.
Η φυσική, όμως, είναι μία κατεξοχήν πειραματική επιστήμη. Οι θεωρητικές υποθέσεις χρειάζονται συνεχή επιβεβαίωση από τα πειραματικά δεδομένα. Το γεγονός ότι, μέχρι στιγμής, δεν υπάρχει δυνατός τρόπος πειραματικής έρευνας σημαίνει πως το πολυσύμπαν, όπως ανέφερα, παραμένει ένα υποθετικό μοντέλο και δεν πρέπει να το δεχόμαστε βιαστικά σαν πραγματικότητα. Μάλιστα, πολλοί φυσικοί έχουν εκφράσει τις αντιρρήσεις τους σχετικά με την ύπαρξη του, αλλά και με την επιστημονική ουσία του, καθώς η αδυναμία πειραματικής εξέτασης αναγάγει την υπόθεση σε φιλοσοφία και όχι φυσική.
Είμαστε, όμως, ανοιχτόμυαλοι άνθρωποι και θα εξετάσουμε την υπόθεση του πολυσύμπαντος με καλή διάθεση. Ας δούμε, λοιπόν, κάποιες βασικές ιδιότητες, με καθημερινή γλώσσα και χωρίς μαθηματικές λεπτομέρειες, αλλά και τις πολύ ενδιαφέρουσες φιλοσοφικές διαστάσεις που παίρνει το θέμα.
Πόσα παράλληλα σύμπαντα υπάρχουν;
Ο επιφανής θεωρητικός φυσικός του MIT, Max Tegmark, το 2003 με την εργασία του “Parallel Universes” [1], διαχωρίζει το πολυσύμπαν σε τέσσερα διακριτά επίπεδα. Ο έτερος φυσικός-celebrity, Brian Greene, έρχεται οκτώ χρόνια μετά, το 2011, να προτείνει την περαιτέρω διαβάθμιση με εννιά(!) διαφορετικούς τύπους, στο βιβλίο του “The hidden reality”. [2] Ουσιαστικά, ο Greene εμβαθύνει στις λεπτομέρειες που διαφοροποιούν τον κάθε τύπο, χωρίς ωστόσο να αψηφά τα επίπεδα του Tegmark. Δηλαδή κάθε τύπος πολυσύμπαντος κατηγοριοποιείται ταυτόχρονα και σε ένα από τα επίπεδα.

Περιληπτικά, τα επίπεδα του Tegmark, όπως αναφέρει η εργασία του, έχουν τις εξής ιδιότητες:
1ο επίπεδο: Περιοχές πέρα από τον κοσμικό μας ορίζοντα
Γράφει χαρακτηριστικά ο Tegmark: “Αν ο χώρος είναι άπειρος και η κατανομή της ύλης είναι αρκετά ομοιογενής σε μεγάλες κλίμακες, τότε ακόμα και τα πιο απίθανα συμβάντα πρέπει να γίνουν πραγματικότητα σε κάποιο σημείο στο χώρο. Συγκεκριμένα, υπάρχουν άπειροι κατοικημένοι πλανήτες, που περιέχουν, όχι μόνο έναν, αλλά άπειρους ανθρώπους με την ίδια εμφάνιση, όνομα και αναμνήσεις με εσάς. Μάλιστα, υπάρχουν άπειρες άλλες περιοχές με το μέγεθος του σύμπαντός μας, όπου εξελίσσεται κάθε πιθανή κοσμική ιστορία”. Σε αυτό το επίπεδο, σύμφωνα με τους τύπους του Greene, ανήκουν τα συρραπτικά, τα πληθωριστικά και τα κυκλικά πολυσύμπαντα.
Αυτό που χαρακτηρίζει κάθε παράλληλο σύμπαν του 1ου επιπέδου είναι το γεγονός πως ισχύουν οι ίδιοι νόμοι της φυσικής, με τη διαφορά πως κάθε σύμπαν έχει διαφορετικές αρχικές συνθήκες. Όλοι οι πιθανοί συνδυασμοί αρχικών συνθηκών, λοιπόν, παράγονται μέσω του κοσμικού πληθωρισμού, δηλαδή μέσω μίας απίστευτα μεγάλης διαστολής του χώρου σε μηδαμινό χρόνο. Οι μικροσκοπικές διαφορές, δηλαδή, ανάμεσα στις αρχικές συνθήκες μεγιστοποιούνται κατά τον πληθωρισμό και ως αποτέλεσμα υπάρχουν ορατές μακροσκοπικές διαφορές στον πραγματικό κόσμο. Άρα κάπου εκεί έξω υπάρχει μία Γη χωρίς εκμετάλλευση, πόλεμο και κοινωνική αδικία. Τα καλά νέα είναι πως αν ισχύουν οι υποθέσεις του Tegmark, μπορείς θεωρητικά να ταξιδέψεις σε αυτό το σύμπαν!
2ο επίπεδο: ‘Άλλες μετα-πληθωριστικές “φυσαλίδες”
Το 2ο επίπεδο αποτελείται από πολυσύμπαντα 1ου επιπέδου, τα οποία αφού περάσουν την πληθωριστική τους φάση, σχηματίζουν “φυσαλίδες”, δηλαδή έναν σχετικά περιορισμένο χώρο. Σε κάθε φυσαλίδα, αν και ισχύουν οι ίδιοι φυσικοί νόμοι, είναι πιθανό να υπάρχουν διαφορετικές φυσικές σταθερές, σωματίδια, ακόμα και χωρικές διαστάσεις. Άρα στο 2ο επίπεδο έχουμε έναν άπειρο αριθμό από διαφορετικά πολυσύμπαντα, το καθένα με άπειρα διαφορετικά σύμπαντα. Εδώ ανήκει το πολύ ενδιαφέρον μοντέλο της Θεωρίας Χορδών, συγκεκριμένα της M-θεωρίας του Edward Witten, το πολυσύμπαν βράνων.
Άπειρο μέσα στο άπειρο; Μας κάνουν πλάκα οι φυσικοί; Μπορεί να φαίνεται αδιανόητη μία τέτοια περίπτωση, αλλά ας δούμε ένα σχετικά πιο εύκολο παράδειγμα. Ας πάρουμε τους ακέραιους αριθμούς. Απλά τα πράγματα, 0, 1, 2, 3 και ούτω καθεξής, μαζί με τους αρνητικούς τους. Όπως ξέρουμε, οι ακέραιοι είναι άπειροι. Ανάμεσα τους, όμως, υπάρχουν οι πραγματικοί αριθμοί, όπως το 1.1, το 1.11, το 1.111 κλπ., οι οποίοι είναι εξίσου άπειροι. Άρα, αφού υπάρχουν άπειροι πραγματικοί ανάμεσα στους ακεραίους και αφού υπάρχουν άπειροι ακέραιοι, οι πραγματικοί αριθμοί είναι απείρως πιο άπειροι από τους ακεραίους, αν μου επιτρέπετε την έκφραση. Κάπως έτσι λειτουργεί το 2ο επίπεδο.
Επιπλέον, σε αντίθεση με το 1ο επίπεδο, η μετακίνηση μεταξύ συμπάντων 2ου επιπέδου δεν είναι δυνατή. Ο χώρος ανάμεσα σε κάθε φυσαλίδα εξακολουθεί να βρίσκεται σε κατάσταση πληθωρισμού και διαστέλλεται με μεγαλύτερο ρυθμό από τον φυσικά επιτρεπτό ρυθμό μετακίνησης της ύλης. Με λίγα λόγια, ακόμα κι αν ταξιδεύεις με την ταχύτητα του φωτός, η απόσταση που πρέπει να διανύσεις αυξάνεται πιο γρήγορα από την απόσταση που καλύπτεις. Σισύφεια η πρακτική, λοιπόν, και δεν προτείνεται από ταξιδιωτικούς οδηγούς.
3ο επίπεδο: Οι πολλοί κόσμοι της κβαντικής φυσικής
Ίσως το πιο δημοφιλές, αλλά και αμφιλεγόμενο, μοντέλο παράλληλων συμπάντων, καθώς συνδέεται άμεσα με την προσπάθεια ερμηνείας της κβαντικής φυσικής και την παράκαμψη της κατάρρευσης της κυματοσυνάρτησης, όπως πρότεινε στη διατριβή του ο Hugh Everett με τίτλο “The many-worlds interpretation of quantum mechanics”. Παραδόξως, αναφέρει ο Tegmark,αν και η ουσία αυτής της υπόθεσης είναι πολύ διαφορετική από τα προηγούμενα επίπεδα, δεν προσθέτει καινούρια συμπαντικά είδη και είναι σε συμφωνία με τα σύμπαντα 1ου και 2ου επιπέδου.
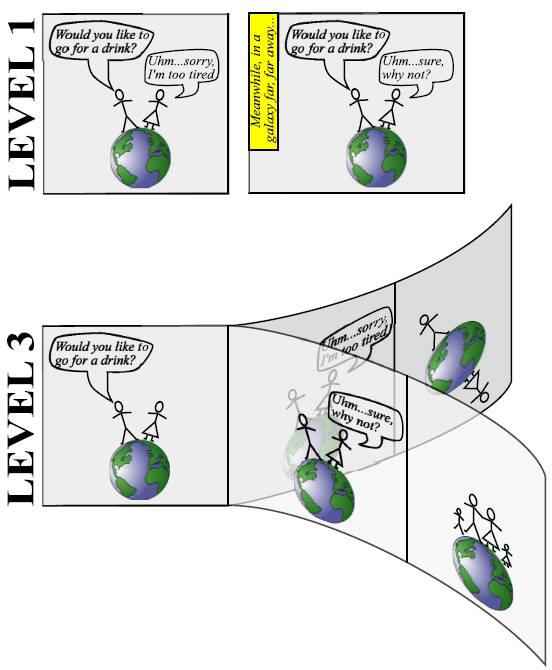
Ο Greene το ονομάζει κβαντικό πολυσύμπαν και είναι το μόνο που ανήκει στο 3ο επίπεδο. Η μεγάλη διαφορά μεταξύ του 1ου και του 3ου επιπέδου είναι η αντίληψη της πραγματικότητας και όχι η ίδια η πραγματικότητα, καθώς και στις δύο περιπτώσεις υπάρχουν όλες οι πιθανές ιστορίες. Στο 1ο επίπεδο είπαμε πως ό,τι μπορεί να συμβεί, θα συμβεί κάπου στο χώρο, πολύ μακριά από μας. Στο 3ο επίπεδο, όμως, ό,τι μπορεί να συμβεί, θα συμβεί ακριβώς εδώ, αλλά σε μία παράλληλη πραγματικότητα. Η σημασία αυτής της διαφοράς παρουσιάζεται πολύ εύστοχα στην παρακάτω εικόνα, η οποία εμφανίζεται και στην εργασία του Tegmark.
Και εδώ βρίσκεται το πιο συγκλονιστικό κομμάτι αυτής της υπόθεσης: κάθε φορά που παίρνεις μια απόφαση, η κβαντική υπέρθεση στην κλίμακα των νευρώνων του εγκεφάλου σου χωρίζει την τωρινή πραγματικότητα σε όλες τις πιθανές διακριτές μελλοντικές πραγματικότητες, όπου η καθεμία δεν μπορεί να γίνει αντιληπτή από τις υπόλοιπες. Δηλαδή σε κάθε σου απόφαση, δημιουργείς έναν ίσως άπειρο αριθμό αντιγράφων του εαυτού σου (!), όπου όλοι έχουν, ή, καλύτερα, έχετε, κοινό παρελθόν, αλλά διαφορετικό μέλλον. Άρα, “εσύ” που αποφάσισες να διαβάσεις το κείμενο μέχρι εδώ, είσαι απλά ένα αντίγραφο αυτού που ήσουν πριν λίγα λεπτά, προτού πάρεις την απόφαση να το διαβάσεις. Υπάρχει, δηλαδή, ταυτόχρονα, σε μία άλλη πραγματικότητα, ένας άλλος “εσύ”, που αποφάσισε να μη το διαβάσει. Αυτός χάνει.
4ο επίπεδο: Μαθηματικό πολυσύμπαν
Η κεντρική ιδέα του μαθηματικού πολυσύμπαντος είναι πως “τα μαθηματικά δεν περιγράφουν απλά κάποιες πτυχές του φυσικού κόσμου, αλλά περιγράφουν όλες τις πτυχές του”. Μπορεί αρχικά να σας φαίνεται απλό, αλλά ουσιαστικά αυτό που περιγράφει είναι πως τα μαθηματικά υπάρχουν εκτός χώρου και χρόνου, ως μία αέναη μοναδική και απαράλλακτη πραγματικότητα. Δύο πολλοί ενδιαφέροντες τύποι 4ου επιπέδου είναι το ολογραφικό πολυσύμπαν και το προσομοιωμένο πολυσύμπαν.
Σε αυτή την περίπτωση, οτιδήποτε έχει φυσική υπόσταση, όπως εγώ κι εσείς, είναι μία πολύπλοκη μαθηματική έκφραση, που απλά έχει την μαθηματική ιδιότητα της αυτο-αντίληψης. Διερωτάται, λοιπόν, ο Tegmark, υπάρχουν μαθηματικές εκφράσεις που δεν έχουν φυσική υπόσταση; Αν υπάρχουν, λέει, αυτό θα σήμαινε πως υπάρχει μία ανεξήγητη και θεμελιώδης ασυμμετρία στην καρδιά της πραγματικότητας, χωρίζοντας τις μαθηματικές εκφράσεις σε δύο κατηγορίες: με φυσική υπόσταση και χωρίς φυσική υπόσταση.
Θέλοντας να λύσει αυτό το πρόβλημα, προτείνει την προσωπική του υπόθεση, την οποία αποκαλεί 4ο επίπεδο ή μαθηματικό σύμπαν. Ορίζει πως η μαθηματική ύπαρξη είναι ταυτόσημη με τη φυσική ύπαρξη, υπάρχει δηλαδή μία σχέση “μαθηματικής δημοκρατίας”. Αν αυτή η υπόθεση είναι σωστή, ουσιαστικά σημαίνει πως, “καθώς δεν υπάρχουν ελεύθερες ή αυθαίρετες παράμετροι, όλες οι ιδιότητες όλων των παράλληλων συμπάντων μπορούν να υπολογιστούν θεωρητικά από ένα απείρως ευφυή μαθηματικό”.
“Φιλοσοφικές” απορίες
Κλείνοντας, θα ήθελα να θέσω δύο προσωπικές απορίες σχετικά με την ελεύθερη βούληση, τις οποίες αποκαλώ “φιλοσοφικές”, καθώς δε θέλω να επεκταθώ σε μαθηματικές λεπτομέρειες, αλλά σε λογικά συμπεράσματα, χρησιμοποιώντας πολύ προσεκτικά τη λέξη “λογικά”. Επιπλέον, σας καλώ να σκεφτείτε πιθανές απαντήσεις, αλλά και να εκφράσετε τις δικές σας απορίες ή αντιρρήσεις.
Αρχικά, θέλω να θίξω τη σημασία της ελεύθερης βούλησης σε όσα διαβάσατε παραπάνω. Ας δεχτούμε πως η υπόθεση του πολυσύμπαντος είναι πραγματική. Είπαμε επανειλημμένα πως ό,τι μπορεί να γίνει, θα γίνει. Συγκεκριμένα, στο 3ο επίπεδο, η θεωρία των πολλών κόσμων αναφέρει πως μέχρι τη στιγμή της απόφασης, το παρελθόν είναι κοινό, άρα υπάρχει μία πραγματικότητα. Μετά την λήψη της απόφασης, όμως, η πραγματικότητα χωρίζεται σε όλες τις πιθανές μελλοντικές πραγματικότητες, λόγω της κβαντικής υπέρθεσης στο ατομικό επίπεδο των νευρώνων.
Και εδώ ακριβώς έρχεται η απορία μου: πήρα συνειδητά την απόφαση ή ήταν οι κβαντικές πιθανότητες που όρισαν τι θα επιλέξω; Ουσιαστικά, αν υπάρχει ελεύθερη βούληση, δε θα έπρεπε να επηρεάζει ένα κβαντικό σύστημα μέσω ενός φυσικού μηχανισμού; Άρα δε θα έπρεπε να έχει φυσική και μετρήσιμη υπόσταση η ελεύθερη βούληση;
Έπειτα, στο ίδιο παράδειγμα, ας δούμε το πρόβλημα από μια άλλη σκοπιά. Είπαμε πως μετά τη λήψη της απόφασης κάθε πραγματικότητα είναι διακριτή και δεν μπορεί να γίνει αντιληπτή από τις υπόλοιπες. Άρα, στο πλαίσιο της προσωπικής μας αντίληψης, σαν ένα από τα αντίγραφα είμαστε μέλη μίας και μοναδικής ιστορίας, στην οποία το παρελθόν είναι απολύτως στατικό και βέβαιο. Δηλαδή δεν υπήρξε ποτέ η πιθανότητα να πάρουμε οποιαδήποτε διαφορετική απόφαση και να βρεθούμε στην πραγματικότητα που βρισκόμαστε σήμερα.
Με αυτή τη λογική, καθώς δε θα αντιληφθούμε ποτέ το διαχωρισμό τον πραγματικοτήτων, δε θα παραμείνουμε για πάντα, ως ένα από τα αντίγραφα, σε μία μοναδική για εμάς πραγματικότητα, στην οποία τα πράγματα δε θα μπορούσαν να είναι διαφορετικά; Τελικά, αφού ό,τι μπορεί να γίνει, θα γίνει, αυτό δε θα σήμαινε πως, για το κάθε αντίγραφο, η τυχαιότητα και η ελεύθερη βούληση είναι απλά μια ψευδαίσθηση;
Πηγές
- Tegmark, Max (May 2003). “Parallel Universes”. Scientific American 288: 40–51.
- Greene, Brian. The hidden reality: Parallel universes and the deep laws of the cosmos. Vintage, 2011.